Rompicapo Quesito: il più semplice problema matematico senza soluzione

Questo quesito viene definito come uno dei buchi neri della matematica, e sembra essere proprio uno di questi casi dove semplice non significa necessariamente facile. Il problema inizia con il fatto che abbiamo molte possibilità di come chiamarlo. Il nome più comune con il quale è conosciuto questo rompicapo è Congettura di Collatz, dal nome del matematico tedesco Lothar Collatz che per primo lo ha proposto nel lontano 1937.

Questo problema irrisolto di matematica è conosciuto anche con altri nomi. Congettura di Ulam per il matematico polacco-statunitense Stanisław Marcin Ulam, il problema di Kakutani per il matematico giapponese-statunitense Shizuo Kakutani, la Congettura di Thwaites per l’accademico britannico Sir Bryan Thwaites, l’algoritmo di Hasse per il matematico tedesco Helmut Hasse. Oppure ancora, il problema di Siracusa.

E questo non è tutto. Alla sequenza di numeri che sono involucrati in questo enigma matematico, viene dato il nome di sequenza dei chicchi di grandine o anche numeri meravigliosi.

Il modo in cui viene definito non è per certo quello che sta facendo diventare pazzi i matematici. In qualunque modo voi lo vogliate chiamare, continua ad essere il problema impossibile più semplice di tutti. Tutti coloro che sanno sommare, dividere e moltiplicare possono capire di cosa stiamo parlando, seguire la sequenza di numeri e persino cimentarsi nell’intento di risolverlo. Però, è dagli anni trenta del secolo scorso che nessuno ha potuto spiegarlo, provarlo o confutarlo.

Pensate che ad un certo momento della storia, si era arrivati a pensare che la congettura era una strategia sovietica per distrarre gli scientifici. Infine, prima di presentarvi il problema, ecco un avviso di uno dei matematici più famosi del ventesimo secolo.

“Le matematiche non sono pronte per questo tipo di problema (…) impossibile, assolutamente impossibile“. Sono le parole del matematico ungherese Paul Erdős, riferendosi alla Congettura di Collatz.

Anche il professor David Eisenbud sulla famigerata Congettura di Collatz, afferma che si tratta di un semplice problema che i matematici potrebbero non essere “pronti” a rompere. Guarda il video.

L’enigma matematico: la congettura di Collatz

Cominciamo con un numero intero naturale (qualunque) 1, 2, 3, 4, 5, 6, 7…

Se il numero è pari, lo dividete per 2
Se il numero è dispari, o moltiplicate per 3 e sommate 1
Poi applichiamo queste stesse semplici regole al risultato.

Cominciamo con 10 che è un numero pari.
10 ÷ 2 = 5, che è un numero dispari, quindi dobbiamo moltiplicarlo per 3 e aggiungere 1.
5 x 3 = 15 + 1 = 16.

16 è un numero pari, quindi dobbiamo fare 16 ÷ 2 = 8
8 ÷ 2 = 4
4 ÷ 2 = 2
2 ÷ 2 = 1
e fino a qui tutto è semplice.

Quello che ci fa lasciare a bocca aperta è il fatto che non importa con quale numero voi cominciate, alla fine si arriva sempre a 4 che poi si trasforma in 2 e quindi finisce con 1. O almeno così fino a questo momento con i numeri che sono stati provati, e sono stati provati anche numeri in alcuni casi assurdi.

Guardate come illustra la questione l’ingegnere di software Jason Davies. Si chiama visualizzazione “grafico Collatz“: tutti i numeri portano al numero uno.

Anche i supercomputer lo hanno fatto arrivando a verificare il questito più o meno fino a questo incredibile numero

5.764.607.500.000.000.000

Tutti i numeri provati alla fine arrivano a 2 ÷ 2 = 1. Nonostante questo, per il fatto che i numeri sono infinti, questo non dimostra che il caso è valido per tutti i numeri naturali. Per il fatto che non è stato possibile trovare una eccezzione, non esiste nemmeno prova che non sia così. Un’altra domanda senza soluzione è l’eterno perchè. Perchè si comportano in questo modo i numeri?

La sequenza dei chicchi di grandine

Abbiamo detto che non importa come, il problema sempre arriva allo stesso punto finale. Il problema è che al momento di cercarlo di risolverlo disegnando un algoritmo, troverete pietre di ghiaccio nel cammino. Come la grandine nelle nuvole prima di cadere, i numeri saltano da un luogo all’altro prima di arrivare a 4, 2, 1.

Chi più, chi meno, senza capo né coda.

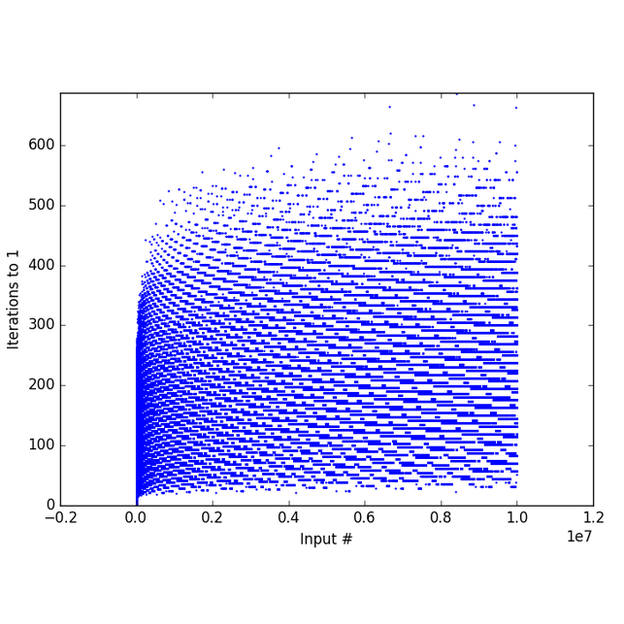Nel grafico qui sopra, vediamo le iterazioni necessarie per arrivare a 4, 2, 1 per i numeri da 2 a 10.000.000. La maggiore quantità di scale che fa un numero iniziale minore di 100 milioni per arrivare a 4, 2, 1 es 986. Però mentre, per esempio, per i multipli di 2 il viaggio è più corto, gli altri hanno bisogno di più tempo.

Un esempio spesso citato è il confronto tra i numeri 8.192 e 27. Il numero 8.192 ha bisogno di 13 passi per arrivare all’inevitabile finale: 4, 2, 1.

Il numero 27 non solo ha bisogno di 111 passi ad arrivare alla fine, ma durante il cammino arriva in alto fino al numero 9.232 prima di arrivare al 8.192 nel 4, 2, 1. La mancanza di “modelli” rende più difficile risolvere una congettura già marcata come impossibile.

Se è davvero così difficile risolverlo (chissà impossibile), vale la pena continuare a tentare?

“Quando si spendono giorni o settimane cercando di risolvere un problema in vano, pensate al povero Sisifo e alla sua roccia” diceva Donald Coxeter, “l’uomo che salvò la geometria”.

“Come il matematico tedesco Felix Behrenddice alla fine del suo libro ‘Sisifo e la sua roccia sono il simbolo dell’uomo e della sua eterna lotta, incessante, irraggiungibile e, tuttavia, sempre trionfante. Che altro si può chiedere?'”

Poetico non trovate? Ma se questo non vi convince dell’importanza di chiarire l’ignoto, chiediamo appello agli esperti di Mathematics Stack Exchange (link), il sito di domande e risposte per le persone che studiano la matematica a qualsiasi livello.

“I matematici sospettano che trovare la soluzione nella Congettura di Collatz aprirà nuovi orizzonti e svilupperà nuove e importanti tecniche nella teoria dei numeri”, dice Greg Muller.

“Il problema di Collatz è abbastanza semplice da capire per chiunque, ma nonostante questo, non solo si relaziona con la teoria dei numeri, ma anche con problemi di decidibilità, il caos e le basi della matematica e informatica. Meglio impossibile”, ha detto Matt.

“Un altro motivo è che, per essere facile da presentare e comprendere, tiene il potenziale per attirare i giovani alla matematica. Io stesso appreso della sua esistenza al liceo, non sono riuscito a resistere al suo fascino”, ha commentato Derek Jennings.

Fonte e adattamento da BBC.